Batch 2 - Class 281 - Behavioral Economics I

Zoom: send meeting Id and password

Start recording

Preclass Exercise:

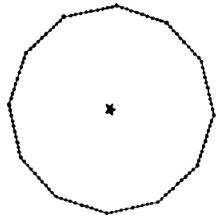
(536Dudeney - 266) An officer wished to form his men into 12 rows, with 11 men in each row, so that he could place himself at a point that would be equidistant from every row. However, there were only 120 men. Was it possible to carry out the order?

Answer: The men may be arranged along rows as shown, with the officer at the center

Attendance: Raghav, Kabir, Shikhar, Ayush, Rhea Chadha, Ryan Chadha, Rohan, Yatharth, Anika, Vansh, Adyant, Siddhant, Dhriti, Ekagra, Aarushi, Mihir, Vivaan, Advay, Aneesh, Siddharth, Harshiet

Class Notes:

Rotating arrows

Take a square piece of card and hold with fingers at diagonal ends. Mark an arrow upwards. Now rotate along the fingers and mark another arrow upwards. As you rotate this the arrow will remain upwards.

Now change the axis of rotation to the other diagonal. What do you observe? Why?

Filling the grid (Contributed by Vansh)

There is a 2xn grid which has to be fully tiled using L shapes (2x2 L) or single dots (1x1). How many ways to tile are there with 2x10 grid

If you take a 2xn grid, the leftmost piece of that can be

Two Ls locked with each other - 2 configurations with (n-3) sized problem left
One L with a dot - 4 configurations with (n-2) sized problem left
Two dots - 1 configuration with (n-1) sized problem left
So F(n)=2(Fn-3)+4F(n-2)+F(n-1)

Double the Pot

Lets play a game. Each of you get five coins of Rs 1 each. Now you can contribute any amount you wish to a pot anonymously. Once everyone has contributed, the amount in the pot will be doubled and distributed equally among all players. You want to maximize the amount of money you are left with.

Let kids play once and see what happens. Allow kids to observe and come to their own conclusions
Let kids play again, and repeat this a few times, say 10 times.
See how the contribution pattern changes, and ask kids to comment on it. Are there kids who contribute a lot initially but then start to contribute less? The other way around?
What is the overall optimal strategy? How do we define an optimal strategy? It is the Nash equilibrium, where no single party has the incentive to deviate from the optimal solution unilaterally. Does this problem have such an equilibrium?
How much of the money you contribute actually comes back to you?

Can you think of other examples where humans don't behave "optimally"?
Aarushi's poser: Pick a number for a lottery. If you pick n, you have chances of winning n with probability of 1/n. What would you pick?

Vansh's rejoinder: "I would pick differently if you allowed me to play the games a million times"

Homework Problem:

In "Filling the Grid" what if its a 3xn grid, with following tiles: 3x2 L and dots - how many ways of filling the grid are there?

References:

Misbehaving, The Making of Behavioral Economics, by Richard Thaler

536 Puzzles and Curious Problems, Henry Dudeney